量子计算模拟编程挑战

作者：dtcxzyw

快速入门 C/CPP

By 赖海斌 12211612@mail.sustech.edu.cn

✅ 温馨提醒

本视频为南方科技大学CS205 C/CPP课程复习课，大家可以作为C/CPP语言的入门视频

背景介绍

~~本人的量子计算知识已经还给老师了，如有错误请指出，不影响做题~~

在经典计算中我们使用比特来表示信息，在量子计算中也有对应的概念，称为量子比特（qubit）。我们使用布洛赫球（Bloch sphere）来可视化单个qubit的状态和相关的计算。单个qubit可以表示为一个单位球面上的点，如下图所示:

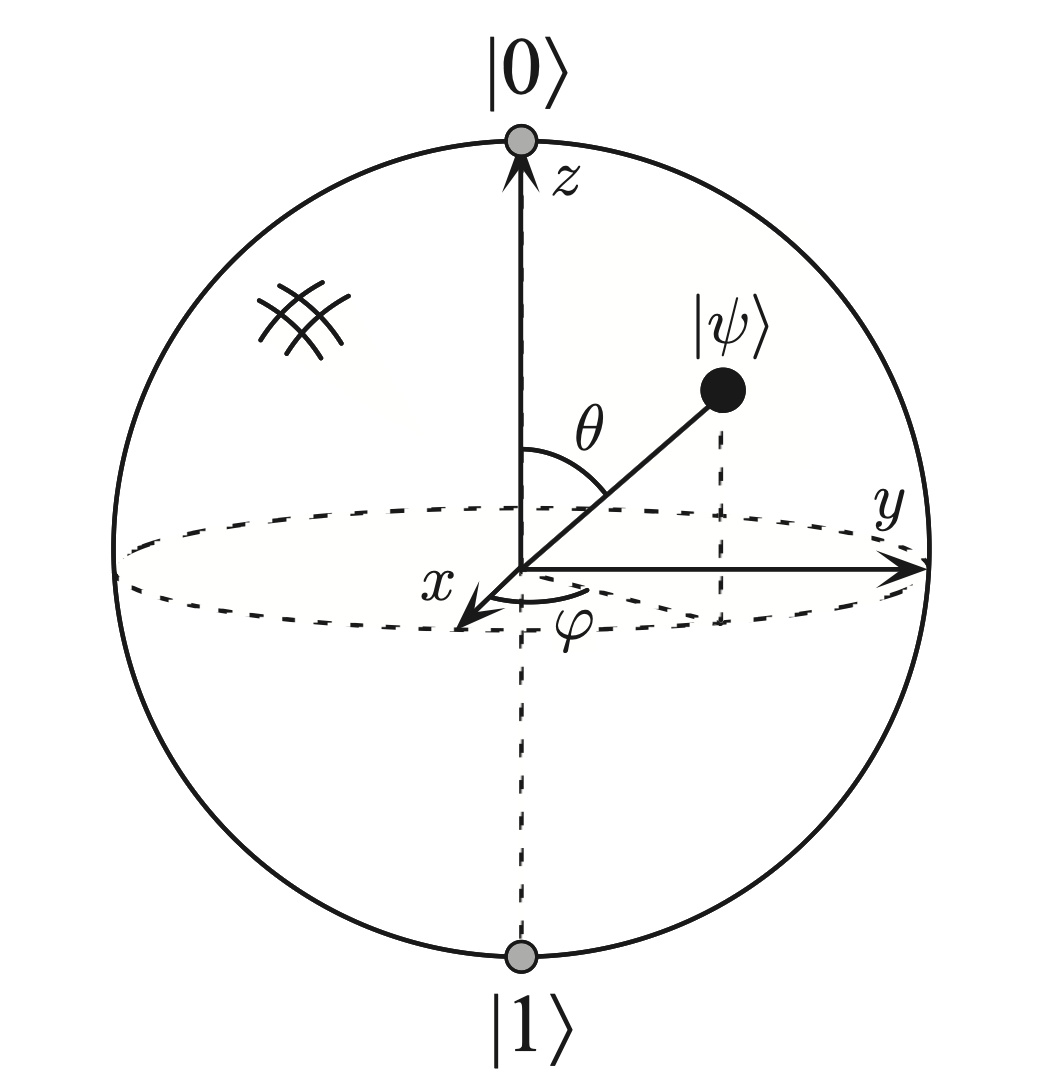
其中 $| 0 ⟩$ 和 $| 1 ⟩$ 是常见的一组基，也就是说我们可以将单个qubit表示为它们的线性组合 $| ψ ⟩ = α | 0 ⟩ + β | 1 ⟩$ ，其中 $α$ 和 $β$ 是复数，满足归一化条件 $| α |^{2} + | β |^{2} = 1$ 。

在介绍完qubit后，我们开始定义量子门（quantum gate）。量子门是对qubit进行操作的基本单元。在理想条件下，我们将作用在单比特上的量子门表示为一个2x2的酉矩阵。常见的量子门包括Hadamard门、Pauli-X门、Pauli-Y门、Pauli-Z门等。XYZ门可以视为在Bloch球上绕X、Y、Z轴逆时针旋转。下面给出各操作对应的矩阵表示：

门类型	矩阵表示
Hadamard门	$H = \frac{1}{\sqrt{2}} [\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}]$
Pauli-X门	$X = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}]$
Pauli-Y门	$Y = [\begin{matrix} 0 & - i \\ i & 0 \end{matrix}]$
Pauli-Z门	$Z = [\begin{matrix} 1 & 0 \\ 0 & - 1 \end{matrix}]$
Phase门	$S = [\begin{matrix} 1 & 0 \\ 0 & i \end{matrix}]$

例如，在对 $| 0 ⟩$ 应用Hadamard门后，我们得到 $H | 0 ⟩ = \frac{1}{\sqrt{2}} (| 0 ⟩ + | 1 ⟩)$ 。

然后我们可以将多个量子门组合起来进行更复杂的操作。最后，我们需要对其量子态进行测量以获取最终结果（qubit->经典bit）。在量子计算机上我们会多次运行量子线路以采样获得测量结果的分布。这一操作可以视为对量子态的投影，我们可以以在 $| 0 ⟩$ 和 $| 1 ⟩$ 为基，将其转换为 $| ψ ⟩ = α | 0 ⟩ + β | 1 ⟩$ 后，观测结果为0的概率为 $| α |^{2}$ 。注意这里的 $α$ 和 $β$ 都是复数，也就是说相位信息被擦除了，感兴趣的同学可以自行了解量子傅立叶变换及其经典应用量子相位估计。

题目描述

本题给出一个单qubit上的量子线路，给定初态 $| 0 ⟩$ ，模拟整个量子线路，计算最终测量前的量子态并以 $| 0 ⟩$ 和 $| 1 ⟩$ 的线性组合表示（~~这里不求测量0的概率以防有人混水摸鱼~~）。

你需要实现一个C++函数，对应签名如下：

cpp

/// \param N 量子门的数量，保证整除于8xCPU逻辑核心数
/// \param Gates 量子门的字符串表示，长度为N，8字节对齐。每个字符表示一个量子门，只可能为'H', 'X', 'Y', 'Z', 'S'中的一个，分别表示Hadamard门、Pauli-X门、Pauli-Y门、Pauli-Z门和Phase门。
/// \param Alpha 输出参数，表示最终量子态的系数$\alpha$
/// \param Beta 输出参数，表示最终量子态的系数$\beta$
void simulate(size_t N, const char *Gates, std::complex<double> &Alpha, std::complex<double> &Beta) {
  ...
}

将该文件命名为simulate.cpp，评测时会将其与driver.o中的入口函数main进行编译链接：

bash

source /work/share/intel/oneapi-2023.1.0/setvars.sh
icpx -std=c++17 -xHost -qopenmp -O3 simulate.cpp driver.o -o simulate

main函数会负责读取输入并调用simulate函数，然后输出结果与运行时间。你只需要实现simulate函数。请不要尝试hack driver.o，最终评测使用的driver.o与提供的预构建二进制文件不同。

该题还提供了生成测试用例的程序gen.cpp，你可以使用以下命令生成测试用例：

bash

g++ -O3 gen.cpp -o gen
./gen N input.bin

然后运行simulate程序来测试你的实现：

bash

./simulate input.bin

参考代码放在位于/work/share/simulate/code-20250626目录下。

样例输入

以N=3，Gates="XHY"为例：

应用Pauli-X门： $| ψ_{1} ⟩ = X | 0 ⟩ = [\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}] [\begin{matrix} 1 \\ 0 \end{matrix}] = [\begin{matrix} 0 \\ 1 \end{matrix}]$

应用Hadamard门： $| ψ_{2} ⟩ = H | ψ_{1} ⟩ = \frac{1}{\sqrt{2}} [\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}] [\begin{matrix} 0 \\ 1 \end{matrix}] = [\begin{matrix} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{2}} \end{matrix}]$

应用Pauli-Y门： $| ψ_{3} ⟩ = Y | ψ_{2} ⟩ = [\begin{matrix} 0 & - i \\ i & 0 \end{matrix}] [\begin{matrix} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{2}} \end{matrix}] = [\begin{matrix} \frac{i}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \end{matrix}]$

故最终结果为 $| ψ_{3} ⟩ = [\begin{matrix} \frac{i}{\sqrt{2}} \\ \frac{i}{\sqrt{2}} \end{matrix}]$ 。可以观察到执行参考例程后输出

Final state: alpha = 0.000000000000 + 0.707106781187i, beta = 0.000000000000 + 0.707106781187i

评分标准

由于最终答案只有几种可能，为了防止大家猜答案，程序会在多组输入下进行正确性验证，若任一输入对应的结果不正确，该题不得分。如果你的程序通过了正确性检验，评测器将执行10个N=2.4*10^10的测试用例并根据几何平均执行时间赋分。该题设置4个检查点，对应不同的考查内容，得分标准如下：

分数	目标执行时间	目标加速比
0	281.56s	1.0
60	8.66s	32.5
80	5.71s	49.3
90	4.68s	60.2
100	1.19s	236.6

评测时程序会在8175m队列上执行，使用的CPU为Intel Xeon Platinum 8175M @ 2.50GHz，具有48个核心（2 Sockets × 24 Cores）。你可以基于使用以下slurm作业模板提交测试任务：

bash

#!/bin/bash
#SBATCH --job-name=sustechhpc-simulate
#SBATCH --partition=8175m          # 提交到 CPU 队列（partition 名）
#SBATCH --nodes=1                  # 所需节点数
#SBATCH --ntasks=1                 # 总任务数（通常 = 核心数）
#SBATCH --cpus-per-task=48         # 每个任务使用的 CPU 核心数
#SBATCH --time=00:10:00            # 最长运行时间（格式：hh:mm:ss）
#SBATCH --output=slurm_%j.out      # 标准输出/错误日志（%j 会替换为作业ID）
#SBATCH --export=NONE              # 不继承环境变量

source /work/share/intel/oneapi-2023.1.0/setvars.sh
./simulate input.bin

如果程序执行时间T落在[L, R]区间内，对应的分数区间为[Lo, Hi], 则得分的计算公式为Lo + (Hi - Lo) * (1/T - 1/R) / (1/L - 1/R)。

备注

参考书籍：Quantum Computation and Quantum Information, Michael A. Nielsen, Isaac L. Chuang
这些量子门的组合有一些特殊的性质，比如HH=I，HXH=Z等。本题允许利用更多量子计算的知识进行加速，但这些不是本题的考察点，即保证不利用这些性质也能拿到满分。
希望大家思考一下如何利用CPU的并行计算能力，想到这一步就有基础分数了。
结果保留到小数点后12位，忽略+0和-0的差异。中间过程避免使用浮点数进行计算，否则可能会因为精度问题导致错误的结果（这里并不是指不能用浮点数）。该题的例程已提供了一个基于符号的计算框架。
最大规模样例输入位于/work/share/simulate/input.bin，对应输出Final state: alpha = 0.000000000000 + -0.707106781187i, beta = 0.707106781187 + 0.000000000000i。
除了提交代码simulate.cpp以外，还需要提交writeup.md描述解答思路以供审查。本题不限制AI的使用（放心我都帮你们试过了），但请在writeup里附上提示词和回答历史记录。

量子计算模拟编程挑战 ​

快速入门 C/CPP ​

背景介绍 ​

题目描述 ​

样例输入 ​

评分标准 ​

备注 ​

量子计算模拟编程挑战

快速入门 C/CPP

背景介绍

题目描述

样例输入

评分标准

备注